| +1515 голосов |
|
Этот мой пост связан с тематикой КО косвенно. Посредством ряда силлогизмов: весьма вероятно, что вы, дорогой читатель, будучи школьником, преуспевали в математике (являющейся основой ИТ, к коим вы, надо полагать, питаете серьезный интерес). А преуспевание в любом деле маловероятно без любви к оному. Следовательно, вы любите математику, и, конечно, неравнодушны к планиметрии, -- прекраснейшему из ее разделов. Так вот; изобретение точного прямила, увенчавшее многолетние и напряженные искания светлых умов прогрессивного человечества, связано с решением планиметрической задачи, которое настолько просто (понимание его требующей лишь знания теоремы Пифагора) и настолько изящно, что в школьные учебники она не попала по недоразумению (впрочем, у прямил имеются и более непосредственная связи с ИТ, но узнать о них смогут лишь те, кто дочитает этот пост до конца).
Итак, дадим для начала строгое определение.
Прямила, суть остроумные, трогательные, радующие глаз и эмоционально заряженные шарнирно-рычажные механизмы, осуществляющие преобразование вращательного движения в прямолинейное (и наоборот). Имея большое практическое значение, они интриговали человечество со времен средневековья.
Чтобы понять, зачем они нужны, рассмотрим два примера.
Пример 1.
Выделенное красным прямило Уатта (того самого) принимает на себя горизонтальные компоненты сил, передаваемых коленвалом на поршень. На определенном этапе двигателестроительного прогресса эти вредные компоненты были одной из ключевых причин исчерпания моторесурса: очевидно, их действие значительно усиливает трение меж боковинами поршня и цилиндра, постепенно трансформируя их сечения в овалы, что нарушает герметичность камеры сгорания, уменьшает эффективность двигателя, и, в конце концов, выводит его из строя (с данной проблемой сталкиваются т.ж. конструкторы паровых двигателей, поршневых насосов и т.п.).
Пример 2 касается систем, оперирующих не кило-, а милливаттами.
Скейтинг (или скатывающая сила) -- понятие из словаря энтузиастов хай-файной техники. Им называют паразитную силу, отклоняющую звукосниматель к центру пластинки при воспроизведении внешних канавок (и, в некоторых случаях, к периферии при проигрывании канавок внутренних). Скейтинга нет лишь на некоторой средней канавке, соответствующей такому положению иглы, из которого центр пластинки и опора тонарма видны во взаимно перпендикулярных направлениях.

Здесь f -- сила трения меж иглой и винилом; F (=f/cos(alpha)) -- усилие, с которым давит на иглу звукоснимателя левая стенка канавки (угол между звукоснимателем канавкой утрирован для наглядности).
Впрочем, вместо того, чтобы раскладывать вектора, объясняющие происхождение скейтинга, можно ограничиться мысленным экспериментом: представьте, что на проигрыватель поставлена пластинка без канавок (напр., круг, вырезанный из листа мелованной бумаги). При попытке его "проигрывания", тонарм под действием скатывающей силы окажется либо у шпинделя, либо спрыгнет с диска, либо перейдет в некоторое среднее устойчивое положение (исход определяется геометрией конкретного тонарма).
Антискейтинговые механизмы (всевозможные грузила и противовесы, устраиваемые в опорной точке) остроумны и разнообразны, но ни один из них не является панацеей (хотя бы потому, что F, очевидно, зависит от текущей конфигурации канавки).
Впрочем, и без скейтинга геометрия обычного (поворотного) тонарма порочна: смещаясь в ходе проигрывания пластинки на +/-~2 см. (для долгоиграющих пластинок это соответствует +/-~0.1 сек.), он проигрывает грамзапись то в ускоренном, то в замедленном темпе. Кроме того, игла, поворачивающаяся вместе с тонармом, почти постоянно оказывается ориентирована под некоторым углом к канавке (в отличие от резца, нарезавшего матрицу, с которой пластинка сделана).
Все это приводит к артефактам, ненавистным уху и уму искушенного меломана. Вот почему в просьюмерском сегменте виниловых проигрывателей получил распространение ряд альтернативных тонармов.

Наибольшую популярность в этом ряду снискали тангенциальные тонармы.

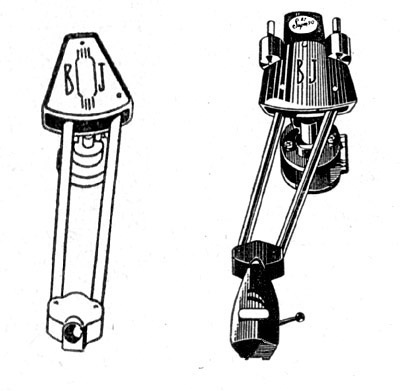
Обычно опора тангенциального тонарма транспортируется линейно вдоль радиуса пластинки электромотором. Мотор производит вибрации и электромагнитные наводки (как кажущиеся, так и реальные), а скорость его движения определяется схемо- и системотехническими решениями, вносящими в тракт проигрывателя (долженствующий быть по возможности нейтральным) дополнительный элемент субъективности. Так что бескомпромиссные поклонники хай-энда никаких моторизированных тонармов не приемлют. Для них производятся безмоторные тангенциальные тонармы с опорными башмаками скользящими на электромагнитной или воздушной подушке (в последнем случае компрессор для подачи воздуха размещается, конечно же, вне комнаты для прослушивания), либо на ультрапрецизионных колесиках, движущихся внутри стеклянной трубы (как в случае с этой моделью Cantus шведской фирмы Rauna).

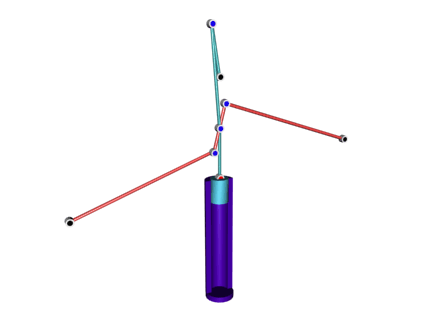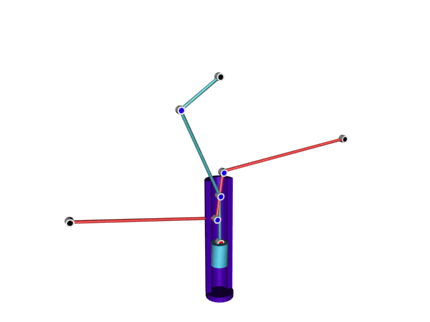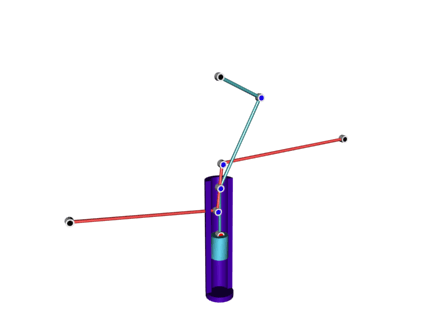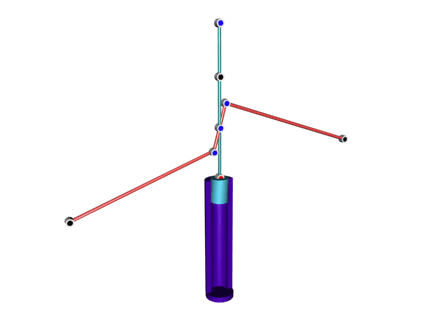
Здесь же надо отметить недавно обретший популярность запатентованный в 2004 г. в Швейцарии "Тонарм Фалеса", названный так в честь одной из теорем Фалеса (провозглашающей прямоту угла, вписанного в окружность и опирающегося на ее диаметр).
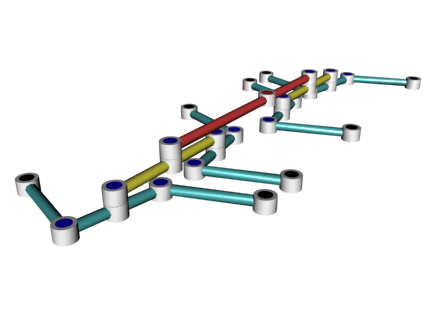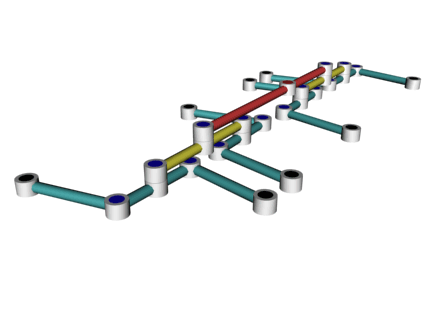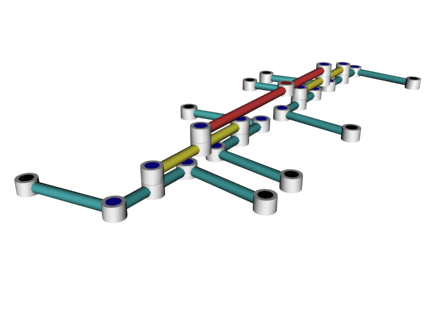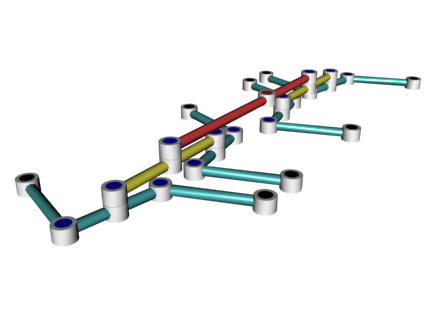
На показанной ниже схеме желтая и красная линии символизируют конструктивные элемента тонарма Фалеса, тогда как черные линии использованы для дополнительных построений.
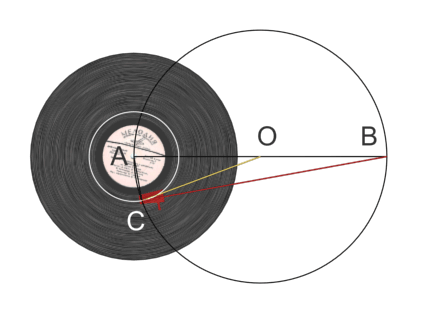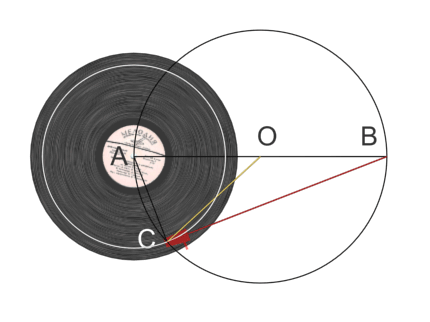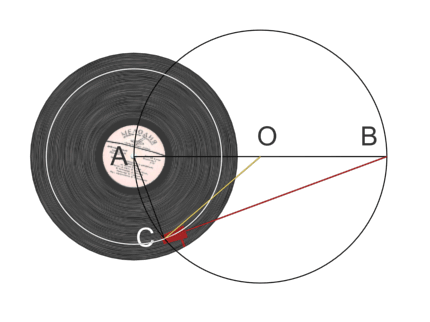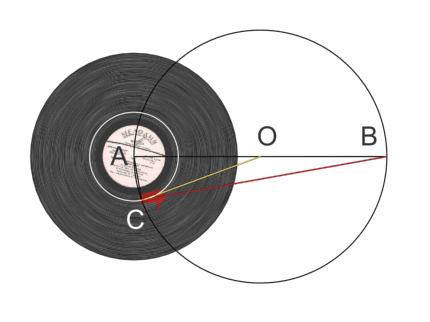
Обратите внимание на то, что красная штанга не сжимается и не растягивается; меняется лишь вид ее вертикальной проекции. В объеме эта конструкция выглядит так:

этот тонарм почти свободен от скейтинга и вообще почти идеален. Но в мире хай-энда "почти" не считается!
Идеальным тонармом могло бы послужить точное прямило, -- т.е., шарнирно-рычажная система, обеспечивающая перемещение звукоснимателя по идеально точной прямой линии, совпадающей с радиусом пластинки. Хотя в настоящее время считается, что резонансные явления в подшипниках многозвенных шарнирно-рычажных механизмов чреваты искажениями, это затруднение, я полагаю, не является принципиально непреодолимым (рискну предположить, что отсутствие на хай-эндовом рынке прямильных тонармов обусловлено не столько обстоятельствами технического свойства, сколько традициями, которые в мире хай-энда не менее сильны, чем субъективизм потребителей).
Однако существуют ли они, идеально точные прямила? Их поиск был в 18-19 вв. сродни штурму проблем философского камня и вечного двигателя или доказательства великой теореме Ферма или попыткам построения сильного ИИ. Внимательный читатель, конечно, обратил внимание на некоторое приукрашивание действительности, к которому я прибег в иллюстрации с поршнем: на ней центральная точка прямила Уатта движется по идеальной прямой. В действительности же она описывает часть "восьмерки" (два участка которой можно считать приближенными к прямым). Эта кривая называется лемнискатой Бернулли (ок. 150 г. до н.э. известной как гиппопеда), и представляет собой геометрическое место точек, для которых произведение расстояний до двух заданных точек ("фокусов") равно квадрату половины расстояния между этими точками. К слову, со времен Др. Греции известно, что гиппопеда является одним из сечений тора:

Самый очевидный (и, очевидно, самый непрактичный) способ повышения точности прямила Уатта состоит в увеличении его размеров.
Еще попытаться составить прямила в иерархию вроде такой:
Увы, в данном случае суперпозиция алгебраических кривых продолжает оставаться кривой.
Одним из исследователей, фанатично проискавших точное прямило всю жизнь, был знаменитый Чебышев. Хотя его усилия успехом не увенчались, он добился впечатляющих результатов в усовершенствовании прямил приблизительных.

А) Прямило Уатта. Первое из документально оформленных прямил (1784 г.), и одно из самых распространенных (ввиду своей простоты).
Б, Д, Е) Усовершенствованные прямила Уатта
В) Одно из множества прямил Чебышева
Г) "Лямбда-механизм" Чебышева
Ё) Прямило Эванса-Дежонжа
Ж) Прямило Робертса
З) Прямило Костицына
Одно из этих приблизительных прямил ("Лямбда-механизм") легло в основу конструкции чебышевского стопохода, который для парижской выставки 1878 в Париже стал примерно тем же, чем для YouTube является Boston Dynamics.
Если стопоход не оставил вас равнодушным, вам стоит ознакомиться с изысканными мобилями Тео Янсена (Theo Jansen).
Появление на свет первого точного прямила исполнено драматизма. О построении инверсора в 1864 году в частном письме сообщил офицер инженерного корпуса французской армии Поселье (Charles Nicolas Peaucellier, умер в 1913 г. в возрасте 90 лет). Однако он не указал никаких подробностей построения механизма. В 1868 году студент Чебышева Йом Тов Липман Липкин (сын знаменитого раввина , умерший в 1876 г. в возрасте 30 лет, -- поразительна разношерстность "прямильщиков"!) изобрёл инверсор. Его подробная статья вышла в 1870 году, и лишь в 1873 году появилась статья Поселье с описанием такого же прямила и со ссылкой на работу Липкина (цит. по www.etudes.ru/ru/etudes/inversor/).
Известно, что Кельвин (тот самый), получив из рук Сильвестра (чим именем названа матрица из всякого курса линейной алгебры) модель оригинального инверсора, принялся ходить с ним по комнате, словно с младенцем, и уговорам отдать его не поддавался:
- Нет, я им еще не насладился. Это -- самое прекрасное, что я видел в жизни!
Легко его понимаю.
Вот примерно пятая часть точных прямил, которые И. И. Артоболевский счел достойными включения в свой ультимативный семитомный трактат "Механизмы в современной технике" (выходивший в переводах и высоко котирующийся в мире).

А) Оригинальный инверсор Поселье-Липкина
Б) Компактный инверсор Поселье-Липкина
В) Прямило Сильвестра-Кемпе (обилие двойных авторств ярко характекризует ажиотаж, сопутствовавший проискам прямил в конце половине 19 века)
Г) Прямило Гарта
Д) А-образное прямило Гарта
Не правда ли, это зрелище напоминает картину из жизни простейших, угодивших в поле зрения микросопа? Аналогия не так уж поверхностна: могие исследоваители избрали прямила в качестве модельных объектов для генетического программирования.
Почему прямило Поселье-Липкина называется инверсором? Дело в том, что ключевая часть этого механизма осуществляет так называемую круговую инверсию плоскости, -- т.е., ее преобразование относительно окружности с центром O и радиусом R, при котором произвольной точке X ставится в соответствие такая точка Y, что:
- Y принадлежит лучу [OX)
- |OX|*|OY| = R2 (т.е., |OX| / R = R / |OY|).
Прошще всего инверсия определяется в полярных координатах: (a,x) <-> (a,R2/x).
Инверсия полезна для решения некоторых планиметрических задач. Она как бы выворачивает круг наизнанку (для оживления лекций преподаватели иногда прибегают к шутке: "Что сделает математик, желающий поймать льва в пустыне? Он построит круглую клетку, запрется в ней и осуществит преобразование круговой инверсии, в результате которго он окажется снаружи, а лев -- внутри").

Картину Вермеера "Географ" я выбрал из-за присутствующего в ней круглого глобуса, позволяющего воочию убедиться в том, что окружности и прямые (напр., края холста) в результате инверсии преобразуются в прямые и окружности. Собственно говоря, любая окружность, проходящая через точку O, отображается в прямую, и наоборот: любая прямая отображается в окружность, проходящую через точку O. Докажем последнее утверждение с помощью несложных планиметрических построений:
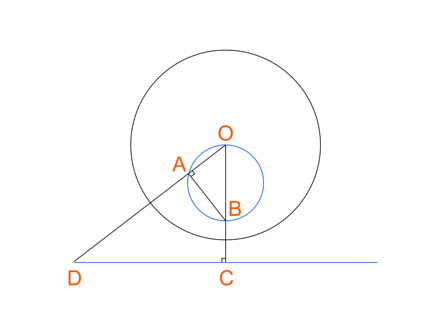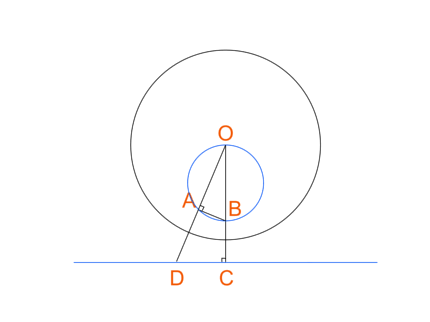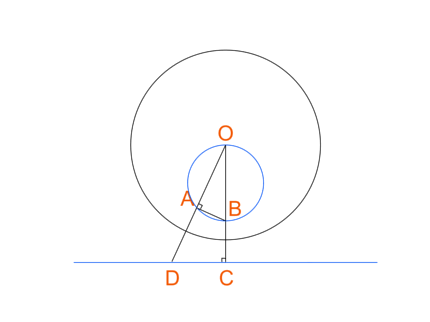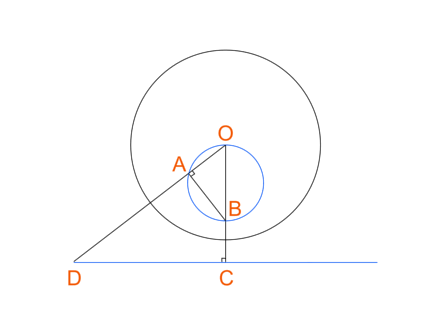
Треугольники ABO и ODC подобны по причине равенства углов: угол O у них общий, а углы A и C -- прямые (C в силу построения, а A -- по пресловутой теореме Фалеса). Это значит, что |OB|/|OD|=|OA|/|OC|, т.е., |OB|*|OC| = |OA|*|OD|, что и требовалось доказать (доказать требовалось не совсем это, но sapienti sat).
Теперь разберемся, действительно ли механизм Липкина является инверсором.

Покажем, что a*b -- величина постоянная и от переменной h независящая.
a = |ОХ|, b = |OY|. Длины этих отрезков равны, соответственно, |OL|-|LX| и |OL|+|LY|. Эти отрезки, в свою очередь, являются катетами прямоугольных трегольников LPO, LPX и LPY, вычислимых по теореме Пифагора.
a*b = ((m2-h2)1/2-(n2-h2)1/2)*((m2-h2)1/2+(n2-h2)1/2) = ((m2-h2)-(n2-h2)) = m2-n2, что и требовалось.
Вот почему введение звена, направляющего точку X по окружности, проходящей через центр круговой инверсии O, заставляет точку Y описывать прямую.
That's all folks!
Нет ли у вас впечатления, что вы ознакомились с чем-то недопреподанным вам в школе? Главной предпосылкой исправления этого общеобразовательного пробела стала возможность сопроводить повествование движущимися картинками. Интересно, в какой мере школьный курс находится в плену традиций, сформировавшихся за нескольлко тысячелетий, в ходе которых этой возсможности у составителей учебников не было, и как долго это довление старины будет сказываться на образовании после тотального вытеснения бумажных учебников электронными.
Увы, не хватило у меня сил сделать иллюстрации еще и интерактивными, хотя технические средства для этого, конечно, имеются. В настоящее время самым удобным средством такого рода для авторов (хотя и не очень удобным для читателей в силу отсутствия интеграции с броузером), по-видимому, является ориентированная на среднеклассников программа редактирования и моделирования 2D-реальности Algodoo. Если вы затрудняетесь с выбором компьютерной игры для ребенка подходящего возраста -- без колебаний устанавливайте ему Algodoo (цена которого, кстати, недавно упала с 11 до 3€). В век, когда виртуальная реальность лишает юных нетизенов сведений о реальном мироустройстве, хорошо довести до них эти сведения хотя бы таким, косвенным путем (да и способность Algodoo содействовать развитию связного мышления представляется неоспоримой).
Не случайно в официальном собрании Algodoo-моделей есть несколько прямил, и возня с шарнирно-рычажными механизмами (см. тут и тут) является одним из излюбленных занятий пользователей Algodoo.
Стратегія охолодження ЦОД для епохи AI
| +1515 голосов |
|




Легко понимаю Вашу увлеченность, широко!!!
Аватара однозначно гармонирует с содержанием данной статьи :)
Это в каком же смысле? Мне не удалось сообщить вам ничего нового и вы статью воприняли как анекдот бородатый?
Нет, исключительно в позитивном смысле, такие длинные и интересные статьи должны писать серьёзные бородатые люди ;)
нет ли в предыдущем посте необоснованного сексизма?
"Интересно, в какой мере школьный курс находится в плену традиций, сформировавшихся за несколько тысячелетий, в ходе которых этой возможности у составителей учебников не было"
У школьного курса нет и не было такой задачи, а вот в курсе ТММ такие возможности ("визуализации") вполне присутствовали.
Но автору об этом знать не обязательно.
интересная статья