|
СПЕЦІАЛЬНІ ПАРТНЕРИ ПРОЕКТУ BEST CIOОпределение наиболее профессиональных ИТ-управленцев, лидеров и экспертов в своих отраслях Человек годаКто внес наибольший вклад в развитие украинского ИТ-рынка. Продукт годаНаграды «Продукт года» еженедельника «Компьютерное обозрение» за наиболее выдающиеся ИТ-товары |
Нейроны, аксоны и универсум дискурса
Автор – Андрей Зубинский, 22 августа 2006 г.
Статья опубликована в №29-30 (549) от 15 августа
Слово «робот» – феноменальное в мире высоких технологий. Феноменальное и тем, что оно имеет славянский корень, и тем, что в интернациональный технический словарь оно попало из художественной литературы (за что земной поклон великому чешскому писателю Карелу Чапеку). Наиболее интересный аспект слова «робот» кроется в его этимологии. Традиционно жизнеспособные слова, становящиеся частью языка и, тем более, многих языков, образуются для обозначения уже существующих предметов. Например, слово «копейка» придумали для обозначения уже существующей монеты – копейной деньги, на которой был отчеканен всадник с копьем. «Компьютером» в свое время, до 1945 г., называли... профессию – тогда computer'ом был человек, работа которого заключалась в решении уравнений. После 1945 г., когда появилась машина, способная заменять человека-вычислителя, традиционное название было адаптировано для нее. И так с подавляющим большинством слов – сначала создавался некий артефакт, затем для него придумывалось название. Но вот с «роботом» все было с точностью до наоборот – сначала благодаря фантастике Чапека появилось слово, оно прижилось практически во всех языках, и только потом, через много-много лет, значение этого слова начало постепенно «овеществляться». Процесс «овеществления» роботов, можно сказать, начался совсем недавно – с тех времен, когда конструкторы получили в распоряжение мощную и доступную элементную базу, компактные и надежные исполнительные устройства, системы проектирования и т. д. И до создания полноценного робота, несмотря на достигнутые успехи (лучшей демонстрацией которых является Honda Asimo), еще очень и очень далеко. В этой статье мы поговорим о двух составляющих алгоритмики, лежащей в основе программного обеспечения самых разнообразных роботов и неисчислимых их «братьев меньших» – различных устройств автоматики. Без этой алгоритмики многие достижения современной робототехники были бы просто невозможны. К несчастью, предмет нашего обсуждения во времена пика его популярности сильно переоценили (не без усилий со стороны бесчисленных коллег по цеху автора этой статьи), что вызвало впоследствии негативное отношение к нему и даже чуть ли не полное забвение. На самом же деле причина и давнишних восхищений, и последующего разочарования обыденна – прописные истины легко забываются, поэтому их надо регулярно повторять: всему есть свое применение, но нет ничего, что было бы применимо всегда и везде. Короче говоря, панацей не бывает. История нечеткой логикиПриблизительно в 400 г. до н. э. Парменид предложил первую версию «Законов мышления», в одном из которых утверждалось, что любое высказывание может быть или истинным, или неистинным. Однако уже тогда не все были согласны с такой детерминированностью. Например, Гераклит предполагал, что существуют утверждения, одновременно истинные и неистинные. Предпосылки для будущей нечеткой логики обосновал Платон, предположивший наличие третьей области между истиной и не-истиной, где эти два понятия перемешаны. Впоследствии многие философы обращались к постулатам Платона (в том числе Маркс и Энгельс), но прикладные теории творят не философы. Сто с небольшим лет назад польский математик Лукашевич описал трехпозиционную логику, в которой третье возможное значение выражения можно описать естественным языком как «возможно». Лукашевич предложил и математическую нотацию, и аксиоматическую систему новой логики. Впоследствии Лукашевич развил свою теорию до многопозиционной логики и даже до бесконечно-позиционной. Интересно, что Дональд Кнут предлагал схожую трехпозиционную логику, для которой вместо «истина, вероятно, ложь» использовал тройку «–1, 0, 1». Трехпозиционная логика Кнута не прижилась и сегодня является просто историческим фактом. А финалом всей этой истории продолжительностью почти в 2 тыс. лет стала публикация в 1965 г. работы Лотфи Заде «Нечеткие множества». Нечеткая логикаО нечеткой (fuzzy) логике мы некогда уже говорили. Но в этой статье без повторений не обойтись. Венец (в прикладном смысле) теории размытых множеств (fuzzy sets) – нечеткая логика – создавалась для моделирования механизма логических выводов «человека как не-computer'а» (в первоначальном значении слова computer), т. е. разумного существа, с легкостью и незаметно для себя оперирующего качественными, а не количественными оценками. В основе моделирования лежит простая и эффективно реализуемая на двоичных последовательных вычислительных машинах алгоритмика лингвистических правил «если – то». При этом ни один из отцов-основателей нечеткой логики (и теории размытых множеств) или признанных специалистов ни разу не был замечен в страшной ереси подмены модели и моделируемого явления. Иными словами, хотя нечеткая логика и позволяет реализовать механизм логического вывода, базирующийся на качественных оценках, это ни в коей мере не означает ни того, что разумные существа мыслят именно на принципе нечеткой логики, ни того, что в ее основе лежат какие-то биологические принципы или аналогии. Эта банальность на самом деле очень важна (как и все банальности в инженерии и науке вообще) – в свое время жадной до околотехнических новостей публике нечеткую логику предъявляли именно как панацею, позволяющую преодолеть барьер детерминированности вычислений, и даже называли «искусственной интуицией». Впоследствии «оказалось», что все это, естественно, чепуха. И наступило некоторое разочарование. Впрочем, это касается только западных школ. Японские инженеры и конструкторы, по-видимому, были менее впечатлительны – по крайней мере, их успехи в робототехнике убедительно доказывают, что нечеткая логика прекрасно работает там, где ей место. А оно давно найдено в самых разнообразных системах управления. Скажем, в простейшей системе управления роботом, на основе которого можно, например, реализовать мечту любого нормально ленивого мужчины – автономный пылесос, убирающий квартиру в отсутствие ее владельцев. Итак, нечеткая логика на примере. Допустим, у нас есть некая гусеничная игрушка с двумя двигателями. Она может передвигаться вперед-назад и поворачивать. Также у нас есть программируемый контроллер, который можно встроить в эту игрушку, способный воспринимать сигналы от датчиков и управлять двигателями. И наконец, у нас есть датчик, способный дистанционно обнаруживать препятствия и грубо определять расстояние до них (например, ультразвуковой локатор). В общем, во всем перечисленном сегодня нет ничего «высокотехнологичного» – это вполне доступно даже при мизерном бюджете. Давайте сразу попробуем поставить себя на место будущего робота и выяснить его представление об окружающем мире. В терминах нечеткой логики это «представление» называется весьма забавно – «универсум дискурса» (universe of discourse), но в русском языке для него принято менее красочное – «предметная область». Итак, об окружающем мире роботу «известно» только то, что может сообщить единственный датчик: есть ли по направлению движения препятствие, и как до него далеко, или просто – расстояние до препятствия (если такового пока нет, то расстояние «бесконечно велико»). О себе самом гусеничный робот без каких-либо иных датчиков, кроме сканера препятствий, может «знать» разве что только направление движения (когда один двигатель выключен, а другой – включен) и собственно факт движения (когда оба двигателя включены – робот движется, когда выключены – стоит на месте). Правила, используемые механизмом логических выводов такого робота, могут, например, описываться следующими предложениями некоторого псевдоязыка, где ЛД – левый двигатель, ПД – правый двигатель, вкл и выкл – «включен» и «выключен» соответственно: IF (расстояние_до_препятствия_бесконечно) THEN (ЛД – вкл, ПД – вкл) IF (расстояние_до_препятствия_больше_N) THEN (ЛД – выкл на 1 секунду, ПД – вкл) IF (расстояние_до_препятствия_больше_M) THEN (ЛД – вкл, ПД – выкл на 1 секунду) IF (расстояние_до_препятствия_меньше_M) THEN (ЛД – вкл, ПД – выкл на 10 секунд)
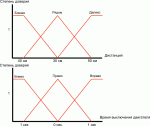
Предположим, что датчик нашего робота способен обнаруживать препятствия на расстоянии, например, 50 см. Тогда все, что находится дальше 50 см, для неподвижного робота не существует. Если теперь принять в предыдущих правилах N=40 см, M=30 см, то можно «на пальцах» смоделировать поведение включенного робота, поставленного в середине пустой комнаты. Согласно первому правилу пока препятствий для робота не существует, он будет передвигаться, не изменяя направления (оба двигателя включены). Если препятствие будет обнаружено, например, на расстоянии 45 см, робот попытается его объехать, повернув влево. Если же препятствие все равно будет приближаться, и расстояние до него станет меньше 40 см, робот «попробует» изменить направление поворота. И наконец, если ничего не поможет, робот развернется (при условии, конечно, что 10 секунд ему достаточно для разворота – последнее правило). То, что мы сейчас описали, пока к нечеткой логике никакого отношения не имеет – это чистая булева логика, универсум дискурса (то, о чем может «поболтать» наш выдуманный робот с нами), которой своей четкостью напоминает наставление по военному делу (рис. 1). Для того чтобы эту «четкую казенщину» превратить в нечто «более интеллектуальное», трансформируем набор правил следующим образом: IF (препятствия_нет) THEN (двигайся_прямо) IF (препятствие_далеко) THEN (поворачивай_влево) IF (препятствие_близко) THEN (поворачивай_вправо) IF (препятствие_рядом) THEN (разворачивайся) Универсум дискурса такой логики выглядит совершенно иначе (рис. 2). Здесь уже присутствует, если можно так сказать, «степень уверенности» в том, что такое, например, «рядом». Ровно 30 см – это «рядом» со степенью уверенности 1, а, например, 33 см – это не совсем рядом, т. е. «рядом» со степенью уверенности где-то 0,7. Введение такой избыточной информации позволяет с помощью несложных математических процедур сравнения степеней уверенности в результатах проверки разных правил формировать усложненное поведение робота. В общем, в нечеткой логике все просто. Кроме одного серьезного нюанса – количества правил. Для более или менее применимого на практике аналогичного робота понадобится, естественно, не один датчик, а несколько, производящих обзор сектора перед роботом. Если для каждого датчика сохранить число правил, равное 4 («препятствия нет», «препятствие далеко», «препятствие близко», «препятствие рядом»), а для исполнительных механизмов ограничиться всего тремя правилами («двигайся прямо», «поворот влево», «поворот вправо»), то количество всех возможных правил, формирующих «интеллект» робота, составит 4N∙32. Например, при шести датчиках правил будет «всего»... 36 864! И тут начинается самое неприятное – ведь никаких формальных способов построения системы правил нечеткая логика проектировщику не предоставляет. Это означает, что fuzzy logic дает только эффективный «исполнительный механизм». А вот что он будет исполнять – задача, средствами самой теории нечетких множеств и нечеткой логики не решаемая. Именно по этой причине в свое время интерес к нечеткой логике быстро утратила не только околотехническая публика, но и специалисты. Программные нейроны и аксоны
Несмотря на заимствованные из физиологии названия, искусственные нейронные сети на самом деле не имитируют естественные нейроны. Первая вычислительная модель нейрона была предложена американскими учеными МакКаллочем и Питтсом в... 1943 г. Да-да, тогда, когда еще не существовало полноценных вычислительных машин. Если не прибегать к графическим моделям, описать искусственный нейрон на уровне более близких любому программисту понятий можно следующим образом – это функция, принимающая переменную-вектор, каждый элемент которого называется «стимулом». Нейрон располагает собственным вектором весов – той же размерности, что и вектор стимулов. Вся «адская механика» внутри искусственного нейрона сводится к довольно тривиальным процедурам – вычислению скалярного произведения векторов стимулов и весов (так называемое «взвешивание»), нахождению суммы элементов полученного вектора, и наконец, использованию найденной суммы в качестве параметра для так называемой функции активации – некоторой нелинейной функции, характеризующей работу всего нейрона. Результат ее вычисления в дальнейшем становится одним из «стимулов» для других нейронов. Казалось бы, совершенно примитивная вещь, реализация которой под силу даже начинающему программисту. И, между тем, этот примитивизм на протяжении почти 60 лет медленно, но уверенно развивается и приобретает популярность. Все дело в том, что искусственные нейронные сети можно «обучать». По большому счету, это означает, что на каком-то заранее известном входном наборе данных (он называется обучающей выборкой) с заранее известными требуемыми реакциями на эти данные можно сформировать нейронную сеть, реализующую эти реакции. Впоследствии же, после такой тренировки (это слово используется в теории нейронных сетей как термин), нейронная сеть может порождать реакции на наборы данных, которые не входили в обучающую выборку. К слову, возвращаясь к устаревшему значению «computer» – нейронные сети, по сути, являются вычислителями, в какой-то мере, но существенно, автоматизирующими решение сложнейших задач, стоящих перед специалистами в области идентификации систем. Потому что построение моделей систем, пригодных для предсказания их реакций на воздействия, для которых реакции не наблюдались, и есть предмет научной дисциплины «идентификация систем». Поразительная общность и примерная одновременность появления компьютеров-устройств и нейронных сетей – весьма примечательный факт. Процедура обучения искусственной нейронной сети заключается в следующем – ей на вход подается выборка данных, для которой заранее известна необходимая реакция системы, и с помощью манипуляций значениями матриц весов отдельных нейронов добиваются требуемого результата. При этом возможны самые разнообразные способы реализации (алгоритмы) того, что мы назвали «манипуляциями». Зависят они прежде всего от топологии нейронной сети. Так, для сетей без обратных связей используются свои алгоритмы, для полносвязных сетей (в которых каждый нейрон соединен со всеми остальными) – свои. Но пока все сети, о которых мы говорили, характеризовались одним общим свойством – им для обучения нужен был кто-то или что-то, обладающее крайне обширными знаниями и готовое поделиться ими с обучаемой сетью. Это нечто принято называть «наставником». По сути, комбинация «наставник» и обучаемая сеть и является заменителем специалиста по идентификации систем – последний, обладая знаниями о системе, пытается построить математическую модель, позволяющую прогнозировать поведение системы за пределами имеющихся знаний о ней, а нейронная сеть, обучаясь на тех же знаниях, сама трансформируется в такую модель, разве что выраженную в специфической форме. То есть в некотором смысле нейронные сети, обучаемые «наставником», ничего существенно нового не принесли. Они сохранили главное – требование к «наставнику» и утрату способности к обучению нейронной сетью, уже выросшей из «учащегося» в работника «на производстве». Во-первых, «наставник» должен очень много знать о моделируемой системе. Чем глубже его знания, тем лучше будет работать обученная им нейронная сеть. Увы, далеко не во всех случаях наличие таких знаний возможно. И, что главное, в большинстве наиболее интересных и полезных применений нейронных сетей получение таких знаний связано с колоссальными рисками или вообще исключено (хотя бы поэтому роботов стремятся применять в первую очередь там и тогда, где и когда участие человека физически невозможно). Ну а во-вторых, уже обученная и работающая в каком-то устройстве нейронная сеть в ходе своей работы ничему больше не учится – то, что в нее заложил «наставник», в нее заложено раз и навсегда. То же самое можно говорить и об особенностях и результатах работы специалиста по идентификации систем – ему также нужны данные, которые в большинстве случаев крайне трудно получить, и построенная им математическая модель в ходе ее эксплуатации сама себя изменять не способна. Довольно долго казалось, что ничего принципиально нового с этими двумя аналогиями, заимствованными из традиционной профессии, сделать невозможно. До тех пор, пока не появились самообучающиеся, или самоорганизующиеся нейронные сети. Обычно класс таких сетей связывают с именем финского ученого Кохонена, но в последнее время созданы обширные классы самоорганизующихся искусственных нейронных структур, например построенных на основе адаптивной резонансной теории. По сути самоорганизующиеся сети обучаются непосредственно в ходе эксплуатации – это огромное их достоинство, достающееся вовсе не бесплатно. Самообучающиеся структуры требуют довольно высокой производительности вычислительных средств в силу большой сложности реализации. Так, искусственная нейронная сеть Кохонена представляет собой двухмерную сеть нейронов, каждый из которых соединен со всеми остальными. Создание такой масштабной системы – далеко не копеечное дело, и без мощных параллельных вычислителей здесь не обойтись, особенно для работы в реальном времени. Кроме того, очевидно, что чем сложнее решаемая задача, тем выше сложность необходимой для ее решения нейронной сети. Из-за этого возникает менее очевидное противоречие – нейронные сети стремятся использовать там, где очень трудно применять традиционные методы идентификации систем, т. е. для решения сложных задач. Соответственно, для этого необходимы сложные нейронные сети и, естественно, мощные аппаратные средства. История реальных нечетких управляющих системВ начале 1970-х годов английский инженер Ибрагим Мамдани (ставший впоследствии специалистом мирового уровня в области нечеткой логики) впервые использовал нечеткие множества в работающей системе управления. При этом к применению нового математического аппарата он пришел не целенаправленно, а случайно. Мамдани пытался создать систему, использующую байесовскую теорию принятия решений, для классической задачи управления паровым двигателем. Мамдани использовал опытного человека-оператора и пытался, наблюдая его реакции, с их помощью обучить байесовский алгоритм. Однако результатом эксперимента стало то, что для решения задач управления подобный подход не годится. Тогда Мамдани попробовал прибегнуть к входящим в моду принципам искусственного интеллекта – экспертным системам, основанным на правилах вывода. И, возможно, благодаря тому, что Мамдани достаточно долго осваивал одну из Lisp-реализаций экспертных систем, ему своевременно попала в руки свежая статья Лотфи Заде – создателя теории нечетких множеств. От этой статьи до реально работающего устройства Мамдани отделяли всего несколько недель. Простота реализации и эффективное функционирование управляющих систем на основе нечеткой логики привели к тому, что всего через несколько лет, в тех же 70-х годах прошлого столетия, на рынке появился первый датский коммерческий нечеткий контроллер для цементного производства. После этого начался настоящий... незаметный расцвет коммерческих «нечетких невидимок» – разнообразных встраиваемых контроллеров, использующих нечеткую логику. Причем расцвет этот наблюдался в основном в Японии. Контроллеры бытовых пылесосов Matsushita и швейных машинок Brother, телевизоров Sony и тормозных систем автомобилей Nissan – все это было реализовано с помощью нечеткой логики. Но японцы пошли еще дальше и отважились на использование fuzzy logic в управляющих системах с очень высокими рисками. Например, в транспортной – в японском городе Сендай с миллионным населением с середины 80-х годов прошлого века «нечеткий» контроллер успешно управляет движением поездов метро. Вслед за японцами к применению нечеткой логики активно подключились и американцы. Так, известная компания Otis выпускает собственные «нечеткие» управляющие системы для лифтов высотных зданий. Но где возможности нечеткой логики и искусственных нейронных систем проявились во всей красе, так это в масштабных системах управления производственными процессами. Например, для планирования сборочного цикла заводов группы SEAT в Марторелле и Наварре, выпускающих соответственно 2000 и 1200 машин в день (здесь нет опечатки). До сих пор никакие иные принципы функционирования систем поддержки планирования, кроме нейронных сетей и нечеткой логики, не позволили сократить обеспечиваемый программными комплексами SEAT пятнадцатиминутный интервал разработки варианта плана. ГибридКак уже говорилось ранее, ни нечеткая логика, ни искусственные нейронные сети никогда не претендовали на моделирование реальных биологических процессов. А вот гибрид этих двух разделов математики позволил сформировать нечто, по мнению многих ученых, хоть чуть-чуть приближенное к основе основ высокоуровневой жизни. А именно, нечеткие искусственные нейроны и сети на их базе. Существует несколько вариантов искусственных нечетких нейронов – они обусловлены обилием возможностей придания «нечеткости» той модели нейрона, которая была описана ранее. Например, с помощью уже известной нам модели достаточно просто и очевидно реализовать правило вида «если – то». Можно заменить детерминированные операции со стимулами и функцию активации на операции нечеткой логики. Но самый многообещающий гибрид нечеткой логики и нейронных сетей на самом деле появляется не посредством объединений теорий и математических аппаратов, а, как это ни странно, на уровне аппаратной реализации спецвычислителей. Дело в том, что нечеткая логика имеет ярко выраженный аналоговый характер (оперирование качественными, а не количественными показателями). Соответственно, аналоговая реализация нечетких нейронных сетей напрашивается сама собой. И кто знает, вполне возможно, что за аналоговым «нейрофаззи»-вычислителем, подключенным к традиционной двоичной детерминированной вычислительной машине, огромное будущее. Стратегія охолодження ЦОД для епохи AI
Читайте также
|
Останні обговоренняТОП-новости
ТОП-блогиТОП-статьи
|
||||||||||||||