|
СПЕЦІАЛЬНІ ПАРТНЕРИ ПРОЕКТУ BEST CIOОпределение наиболее профессиональных ИТ-управленцев, лидеров и экспертов в своих отраслях Человек годаКто внес наибольший вклад в развитие украинского ИТ-рынка. Продукт годаНаграды «Продукт года» еженедельника «Компьютерное обозрение» за наиболее выдающиеся ИТ-товары |
Квантовые информационные технологии
Автор – Елена Гомонай, 12 февраля 2003 г.
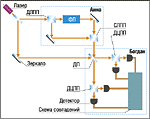
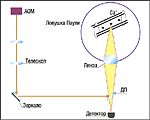
На заре эпохи интегральных микросхем, в 1965 году, будущий сооснователь компании Intel Гордон Мур предсказал удвоение плотности транзисторов в полупроводниковых микросхемах через каждые 18 месяцев. Закон Мура выполняется уже в течение 37 лет, и сегодня размеры элементов транзистора составляют четверть микрона. Возникает вопрос о принципиальных ограничениях на размеры логических вен-тилей и возможности реализации вычислений на квантовых системах. Одним из первых об ограничениях, следующих из квантовой механики, задумался известный физик Ричард Фейнман (Richard Feynman). Он установил, что, если рабочие части компьютера сделаны из атомов, кроме очевидного ограничения на размер, никаких фундаментальных ограничений не существует. Однако возможно ли создать компьютер, в котором поведение системы битов будет определяться законами квантовой механики? Вычислительный процесс всегда рассматривался как чисто классический. Другими словами, в процессе вычислений предполагается, что состояние отдельного бита однозначно определено и может быть установлено на любой стадии вычислений, а результат операции, выполняемой над отдельным битом, предсказуем. Считывание информации не влияет на состояние бита, а физическая реализация логической операции -- на результат вычислений, что позволяет рассматривать этот процесс независимо от аппаратного воплощения. В противоположность этому в основе квантовой механики лежат принцип неопределенности Гейзенберга и вероятностный характер состояний квантовых систем. При измерении (считывании) состояние квантового объекта (бита), как правило, изменяется. Все это, казалось бы, находится в противоречии с требованием полной определенности и однозначности классических вычислений. Бенефф выдвинул идею универсального квантового компьютера -- машины, которая выполняет логические операции, опираясь на квантовые алгоритмы, не имеющие аналогов в классической физике, и способна решать любые (а не только специализированные) задачи. Фейнман показал, что квантовый компьютер для ряда задач является более мощным, чем классический, а Дойч разработал идею квантового параллелизма. Таким образом, эти ученые заложили фундамент новой современной области исследований -- квантовых информационных технологий, или квантовой информатики. Квантовая информатика в полной мере использует такие свойства квантовых объектов, как суперпозиция состояний, способность системы из нескольких частиц находиться в коррелированных, или "перепутанных состояниях" (entangled states), существенное влияние процесса измерения на состояние объекта, невозможность клонирования квантовых состояний. Одной из наиболее разработанных областей применения квантовой информатики является криптография. Основные направления применения криптографических методов -- передача конфиденциальной информации по открытым каналам связи (например, через Internet), а также установление достоверности передаваемых сообщений. Свойство квантовых объектов изменять состояние при измерении как нельзя лучше подходит для обеспечения секретности передаваемых по открытым сетям сообщений. Первый криптографический протокол обмена данными, основанный на квантовых свойствах фотонов, был придуман Чарльзом Беннетом (Charles Bennett) и Жилем Брассаром (Gilles Brassard). Он был назван в их честь ВВ84 и вошел практически во все публикации, посвященные квантовой криптографии. Здесь мы рассмотрим другой, не менее изящный, протокол, придуманный теми же авторами. Он основан на свойствах перепутанных состояний. Пару фотонов, находящихся в перепутанных состояниях, можно получить в процессе так называемой параметрической генерации света: кристалл с нелинейными оптическими свойствами, скажем, KNO3, облучают лазерным излучением видимого диапазона (длина волны 655 нм), а на выходе получают два инфракрасных пучка (длина волны 1310 нм). То есть из одного оптического фотона образуются два связанных инфракрасных. Особенность данного процесса заключается в том, что о получаемой на выходе паре фотонов точно известно, что поляризации фотонов (обусловливающие их состояния) взаимно перпендикулярны, однако какой из двух полученных фотонов в каком состоянии находится -- неизвестно. Если измерить состояние поляризации одного из фотонов, то можно мгновенно узнать и состояние второго, не делая никаких дополнительных измерений (конечно, если заранее известно, каким образом получались фотоны). Такие фотоны называют перепутанными. Они обладают еще более интересными свойствами. Так, если заранее не знать, как приготовлялись фотоны, то измерение состояния каждого из них в отдельности не дает никакой информации о системе в целом, однако совместное измерение, выполненное над парой фотонов, однозначно определяет их состояние. Кроме того, воздействуя на один фотон из пары, можно менять состояние пары целиком. Как же можно использовать на практике это свойство фотонов? Рассмотрим схему, изображенную на рис. 1. Допустим, Анна хочет передать секретную информацию Богдану. Для этого Богдан создает у себя пару фотонов в перепутанных состояниях, один из них оставляет у себя (например, пускает бегать по очень длинному оптоволоконному кабелю), а второй отправляет Анне. Анна с помощью специальных оптических приспособлений (поляризаторов и приборов для смещения фазы) воздействует на фотон и таким образом меняет состояние всей пары, а после этого отсылает "обработанный" фотон Богдану. Тот получает "шифрованный" фотон и проводит измерение над парой фотонов (своим и Анны), однозначно определяет состояние пары и расшифровывает информацию. При этом, поскольку система из двух фотонов может находиться в одном из четырех состояний, передаваемая таким образом информация составляет 1,58 бит (исходное состояние может быть изменено тремя способами), в отличие от 1 бита, который передавался бы при работе с классическими объектами. Кроме существенного уплотнения информации, такая схема устойчива по отношению ко взлому. Действительно, если нарушитель пытается перехватить сообщение, посылаемое одной из сторон, он вынужден измерять состояние только одного фотона из пары. Таким образом он, во-первых, не получает никакой информации (в силу свойства перепутанных фотонов нести информацию только парами), а во-вторых, нарушает когерентность и перепутанность пары и обнаруживает себя. Конечно, реализация такой схемы обмена данными требует возможности оперировать чрезвычайно слабыми световыми пучками (содержащими один фотон). Тем не менее технические препятствия в настоящее время достаточно успешно преодолеваются. Наиболее перспективными в этом отношении считаются сигналы с длинами волн 1300 и 1550 нм (лазеры и детекторы на основе InGaAs), которые могут обеспечить передачу маломощного сигнала на расстояние до 60 км (Женевской группе удалось обменяться однофотонными сигналами с помощью оптического кабеля длиной в 20 км, проложенным под Женевским озером, а Лос-Аламосская группа сообщала о передаче сигнала на 58 км, однако кабель при этом полностью находился в помещении лаборатории). Особые свойства перепутанных состояний могут помочь также в осуществлении процессов переноса информации в квантовых компьютерах. Для таких процессов употребляют термин, придуманный писателями-фантастами, -- телепортация. Телепортация означает исчезновение объекта в одном месте и появление точной его копии в другом, короче говоря, перенос состояния материального объекта по информационным каналам. Телепортировать классический (материальный) объект невозможно -- для этого бы понадобилось опуститься на квантово-механический уровень, а здесь точности измерений препятствует принцип неопределенности Гейзенберга. Однако именно квантовая механика указывает способ телепортации состояния объекта без непосредственного его измерения, а это именно то, что требуется при передаче информации (нас ведь интересует состояние бита -- 0 или 1, а не то, является бит магнитным доменом или просто электрическим конденсатором). Впервые этот факт был установлен все теми же Беннетом и Брассаром в 1993 г., а экспериментально процедура телепортации осуществлена Цайлингером (А. Zeilinger) с сотрудниками в 1997 г. Для того чтобы понять, как проходит телепортация, заметим, что состояние квантовой системы обычно описывают как вектор в так называемом гильбертовом пространстве (полном евклидовом пространстве). Базисом в нем служит полный набор состояний системы, которые мы можем установить с помощью наших приборов, а проекция на базисные векторы определяет амплитуду вероятности обнаружить частицу в заданном базисном состоянии. Например, если речь идет о состоянии фотона, то базис определяется ориентацией поляризатора. Вертикальная и горизонтальная поляризации образуют двумерный базис, а состояние фотона можно представить как суперпозицию обеих поляризаций (для системы из N фотонов размерность базиса будет 2N). Теперь обратимся собственно к процедуре квантовой телепортации. Предположим, Анна хочет переслать Богдану информацию о фотоне Х, причем состояние фотона неизвестно. Для этого производится следующая процедура. Создается пара фотонов, 1 и 2, в известном перепутанном состоянии. Один фотон из пары отсылается Богдану, а второй -- Анне. Анна сводит вместе два фотона -- 1 и Х -- и производит над ними такое измерение, чтобы оба фотона при этом перешли в известное перепутанное состояние, в котором до этого была пара фотонов 1 и 2. При этом мгновенно фотон 2, находящийся у Богдана, переходит в неизвестное состояние Х! Предупредим естественный вопрос читателя -- не обеспечивает ли мгновенное изменение состояния фотона 2, находящегося у Богдана, возможности передачи сигналов со сверхсветовой скоростью, что противоречит основному постулату теории относительности. Никаких нарушений известных принципов не происходит -- результат измерения, производимого Анной, носит вероятностный характер, и телепортация нужного состояния может произойти не с первой попытки. Для того чтобы сообщить Богдану об успешном завершении телепортации, Анна должна воспользоваться классическим каналом связи, что исключает сверхбыстрый обмен информацией. Усложненная процедура телепортации, включающая большое число фотонов, может оказаться удобной для аутентификации или для одновременного "вскрытия" документа разными пользователями. Это связано с так называемым процессом удаленного переключения состояний, описание которого выходит за рамки этой публикации. Обратимся, наконец, к квантовым вычислениям и устройству квантового компьютера. Идея квантовых вычислений была высказана еще в начале 80-х годов, однако реально только в 1994 г. Питер Шор (P. W. Shor) предложил эффективный квантовый алгоритм решения задачи о факторизации (разложении на множители) больших чисел, а также вычисления дискретных логарифмов, а Цирак (J. I. Cirac) и Золлер (P. Zoller) продемонстрировали возможность аппаратной реализации такого рода вычислений с использованием охлажденных ионов 40Са+ в магнитной ловушке. Современные достижения в области микроэлектроники и материаловедения позволяют надеяться на возможность реализации квантового компьютера на полупроводниковых кристаллах с так называемыми квантовыми точками, квантовыми нитями и колодцами и т. п. Сама идея квантовых вычислений достаточно проста. В обычных классических компьютерах приходится иметь дело с ячейками памяти и элементами логики, которые содержат только один бит информации и могут находиться в одном из двух состояний -- "0" или "1". В квантовом компьютере элементарной единицей информации является кубит (qubit), т. е. квантовый бит -- термин, введенный в 1995 г. Бенджамином Шумахером (Benjamin Schumacher). Кубит представляет собой квантовую двухуровневую систему, которая может находиться не только в состояниях |0> и |1> (здесь использованы обозначения квантовых состояний, введенные Полем Дираком), но и в суперпозиции этих состояний. Научившись оперировать с кубитами, можно достичь невероятного ускорения процесса вычислений для некоторого класса задач. Рассмотрим в качестве примера квантовый алгоритм Гровера (Grover) -- поиск по базе данных. Предположим, нам необходимо выяснить, кому принадлежит номер телефона 101001...001 (в двоичной системе). Если в "телефонном" справочнике зарегистрировано 1 млн. абонентов, то, пользуясь простейшим классическим алгоритмом поиска, нам потребуется выполнить порядка миллиона операций (если, конечно, не сильно повезет), поскольку придется просматривать последовательно все номера и соответствующие им фамилии. В случае, если поиск осуществляется посредством квантового компьютера, информация шифруется с помощью вектора состояния, номера телефонов соответствуют базисным векторам, а фамилии абонентов кодируются проекциями вектора состояния системы на базисные векторы. Для того чтобы по заданному номеру телефона определить абонента, необходимо вычислить проекцию вектора состояния системы на заданную ось. Расчет показывает, что для успешного выполнения такой процедуры достаточно произвести порядка 1000 операций! Еще более впечатляющим является алгоритм Шора факторизации больших чисел. Следует подчеркнуть, что в современной криптографии стойкость процедуры шифрования по отношению ко взлому основывается на невозможности решить ту или иную математическую задачу за приемлемое время. Одной из таких задач является разложение на множители больших чисел -- число операций, необходимых для ее выполнения, экспоненциально растет с увеличением числа знаков в факторизуемом числе. Использование квантовых алгоритмов позволяет решить эту задачу за полиномиальное число шагов. Реализация квантового компьютера с достаточно большим числом кубитов может, таким образом, создать серьезные проблемы для криптографов (и значительно облегчить труд криптологов!). Что же такое все-таки квантовый компьютер? Для того чтобы построить универсальную вычислительную машину, необходимо иметь носитель информации (набор битов или кубитов), уметь физически выполнять логические операции, передавать их результат от бита к биту и вводить/выводить информацию. Кроме того, логические операции должны быть обратимыми, и их набор -- достаточным для выполнения любого математического действия (на самом деле такая возможность обеспечивается наличием операции "исключающего ИЛИ" -- XOR). Оказывается, всем этим требованиям можно удовлетворить, работая с квантовыми объектами. Собственно носителями информации (кубитами) могут выступать любые достаточно стабильные двухуровневые системы, например атомы, ионы, электроны в квантовых точках и др. Квантовые логические вентили реализуются как унитарные (обратимые) преобразования над кубитами, которые можно осуществлять с помощью лазерных импульсов с правильно подобранной продолжительностью и несущей частотой. Их обратимость гарантируется природой квантовой механики. Имея логические вентили с одним или двумя кубитами, можно построить логические схемы любой архитектуры. Особой проблемой квантового компьютера является ввод/вывод информации. В отличие от классических систем ввод/вывод означает преобразование информации квантовой формы в классическую и наоборот. Такая процедура предусматривает физическое измерение состояния объекта, которое в квантовой механике может изменить состояние, да и сам объект. Тем не менее известны неразрушающие измерения, например флюоресценция атомов при переходе с одного из возбужденных (информационных) уровней на основной, для ряда систем допустимы многократные измерения результата вычислений; в любом случае считывание информации с квантового компьютера требует дополнительной ее обработки классическими методами. Остановимся, наконец, на еще одной важной проблеме, относящейся к квантовым вычислениям, -- нарушении когерентности и коррекции ошибок. Ошибки и сбои, связанные с непредсказуемым изменением состояния бита, присущи любому вычислительному устройству, однако квантовые системы гораздо более чувствительны к воздействию окружающей среды, нежели классические. По этой причине все системы, которые считаются перспективными с точки зрения квантовых вычислений, работают при очень низких температурах, в вакууме, в общем, в жесткой изоляции (тем не менее не следует представлять себе при этом конструкции размером с трехэтажный дом -- установка, работающая с охлажденными атомами, легко размещается на столе, а требуемый вакуум достигается после часа работы). Однако даже при этом когерентные состояния живут около секунды (что, правда, позволяет осуществить миллион операций), а потом начинаются сбои. Эффективное время работы состояний можно существенно продлить, если ввести процедуру коррекции ошибок. Классическая коррекция ошибок основывается на введении дополнительных "контрольных" битов, например бита четности, и на регулярной проверке состояния этих битов в процессе вычислений. В квантовых вычислениях любое дополнительное считывание информации рискует разрушить всю систему, поэтому явное выяснение результата промежуточных вычислений нерационально. Однако есть другая возможность, предложенная Шором и Стином (A. M. Steane). Она также основана на избыточном кодировании исходной информации. Например, вместо одного кубита используют три: состояния a|0>+b|1> кодируют векторами состояний a|000>+b|111>. Обработка информации построена таким образом, чтобы под действием логических вентилей все три информационных кубита изменялись одинаково. Нарушение когерентности может привести к изменению состояния одного из кубитов, например |000> |010>. Для определения ошибки выясняют, находятся ли все три частички (кубиты) в одинаковом состоянии или нет, при этом не определяя самих состояний. При выявлении ошибки ее легко исправить, изменяя состояние одного из кубитов. Квантовая коррекция ошибок, хоть и требует значительного дублирования информации и, как следствие, увеличения оперативного объема системы, позволяет значительно продлить процесс вычислений и сделать работу квантового компьютера почти независимой от влияния внешней среды. Сегодня квантовая информатика представляет собой открытую для исследований и быстро развивающуюся область на стыке наук. Станет ли XXI век веком квантовых компьютеров или в результате изучения старых дисциплин в новом ракурсе возникнут новые принципы обработки, передачи, систематизации информации, а возможно, и новые методы ее усвоения -- неизвестно. Однако уже с 1998 г. курс "Основы квантовой информатики" вошел в учебные планы ведущих технических вузов как часть дисциплины "Теоретическая физика". Стратегія охолодження ЦОД для епохи AI
Читайте также
|
Останні обговоренняТОП-новости
ТОП-блогиТОП-статьи
|
||||||||||