Ученые подвергают сомнению принцип неопределенности Гейзенберга

Принцип неопределенности Гейзенберга, сформулированный в 1927 г., является одним из краеугольных камней в квантовой механике. В наиболее простом изложении он говорит о том, что любое измерение в квантовой механике оказывает влияние на измеряемый объект. Например, попытка измерить положение частицы может случайным образом изменить ее импульс.

Этот принцип околдовывал физиков почти столетие, когда недавно ученые из Торонтского университета продемонстрировали возможность прямо измерить возмущение и подтвердить, что Гейзенберг был слишком пессимистичен.

«Мы разработали прибор, чтобы измерить поляризацию единичного фотона. Затем нам нужно было измерить, насколько сильное влияние прибор оказал на состояние фотона, — сказал д-р Ли Розема (Lee Rozema). — Чтобы сделать это, нам нужно было определить состояние фотона перед измерением, но это бы внесло возмущение».

Для того чтобы преодолеть это препятствие, ученые использовали технику, известную как слабое измерение, в котором действие измеряющего устройства достаточно слабо, чтобы оказывать существенное влияние на измеряемую величину. Перед тем как единичный фотон направлялся в измерительную аппаратуру, исследователи проводили слабое измерение, а затем делали еще одно измерение и сравнивали результаты. Они обнаружили, что возмущение, вносимое измерением меньше, чем предсказывают неравенства Гейзенберга.

«Каждый выстрел фотоном давал нам крупицу информации о возмущении, но повторяя эксперимент много раз, мы пришли к очень хорошей идее, насколько сильно был фотон возмущен», — сказала д-р Розема.

Открытие поддерживает последние претензии к принципу Гейзенберга, появившиеся у многих ученых. Масанао Одзава (Masanao Ozawa), физик из Университета Нагойи, в 2003 г. предположил, что принцип неопределенности не применим к измерениям, но в то время он мог предложить только непрямой метод подтверждения своей гипотезы. Предложенная им проверка была выполнена в прошлом году группой Юджи Хасегава (Yuji Hasegawa) из Венского технологического университета. В 2010 г. ученые Остин Лунд (Austin Lund) и Говард Уайзмен (Howard Wiseman) из Университета Гриффита, Австралия) показали, что слабые измерения могут использоваться для описания процесса измерения в квантовых системах. Однако это трудно было проверить, так как их идея по сути требовала небольшого квантового компьютера, построить который тогда не представлялось возможным.

«В прошлом мы работали как над реализацией слабых измерений, так и над использованием техники, называемой квантовые вычисления на кластерных состояниях (тип состояния множества кубитов с сильным зацеплением), чтобы упростить построение квантовых компьютеров. Комбинация этих двух идей привела к осознанию того, что имеется способ реализовать идеи Лунда и Уайзмена в лабораторных условиях», — объяснил д-р Розема.

Часто предполагается, что принцип неопределенности Гейзенберга применим как к присущей квантовой механике неопределенности, которой должна обладать квантовая система, так и к измерениям. Полученные результаты показали, что это не так в последнем случае, и продемонстрировали степень точности, которая может быть достигнута при применении техники слабого измерения.

«Эти результаты заставили нас изменить взгляд на пределы точности измерений, которые устанавливает квантовая механика, — сказал д-р Розема. — Эти пределы важны для оснований квантовой механики, а также для разработки технологий квантовой криптографии, которые опираются на принцип неопределенности».

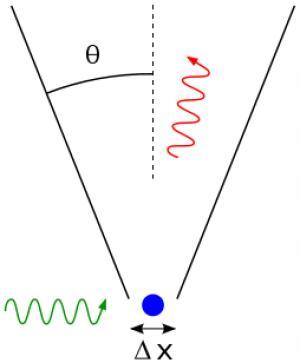
Гейзенберговский гамма-микроскоп, используемый для определения координаты электрона (показан синим). Входящие гамма-лучи (зеленые) рассеиваются электроном на угол, равный апертуре микроскопа (рассеянные гамма-лучи показаны красным). Классическая оптика показывает, что положение электрона может быть определено только с неопределенностью Δx, которая зависит от угла Θ и длины волны падающего света

Ready, set, buy! Посібник для початківців - як придбати Copilot для Microsoft 365