|
СПЕЦІАЛЬНІ ПАРТНЕРИ ПРОЕКТУ BEST CIOОпределение наиболее профессиональных ИТ-управленцев, лидеров и экспертов в своих отраслях Человек годаКто внес наибольший вклад в развитие украинского ИТ-рынка. Продукт годаНаграды «Продукт года» еженедельника «Компьютерное обозрение» за наиболее выдающиеся ИТ-товары |
Сетевое кодирование
Автор – Леонід Бараш, 2 марта 2009 г.
Статья опубликована в №5 (671) от 17 февраля
Когда речь идет о повышении пропускной способности сети, то обычно говорят о более быстрых интерфейсах, агрегировании трафика, плотном мультиплексировании и других аппаратных решениях. Однако поднять производительность сети (речь идет не о повышении скорости работы сетевых приложений) можно и без радикальных изменений в инфраструктуре. Одним из способов достичь этого является сетевое кодирование, которое особенно эффективно при многоадресных передачах.
Сегодня сетевые коммуникации базируются на одном и том же фундаментальном принципе работы. Во всех случаях, будь-то передача пакетов через Интернет или сигналов по телефонной сети, информация транспортируется подобно тому, как автомобили разделяют автомагистраль или потоки – трубопровод. Другими словами, потоки данных могут использовать общие сетевые ресурсы, однако информация в них не смешивается. Маршрутизация, хранение данных, контроль ошибок и в конечном итоге все сетевые функции основываются на этом предположении.
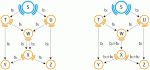
Данную концепцию нарушает сетевое кодирование (network coding) – новое направление в теории информации, позволяющее достичь максимального потока информации в сети. Оно предполагает, что узлы вместо обычной передачи пакетов могут комбинировать несколько входных пакетов в один или в несколько выходных. Эту идею можно проиллюстрировать простым примером из беспроводных коммуникаций. На рис. 1 узлы А и В хотят обменяться пакетами через базовую станцию S. При традиционном методе А и В посылают S соответственно пакеты а и b, а затем S выполняет их широковещательную рассылку. Таким образом, узел А (соответственно узел В) получает ненужный ему собственный пакет, а обмен пакетами занимает четыре цикла передачи. При использовании сетевого кодирования станция S, получив пакеты a и b, посылает результат выполнения над ними операции XOR (исключительное ИЛИ). Узлы затем могут извлечь интересующие их пакеты из результирующего, а обмен данными выполняется только за три цикла. Линейное сетевое кодирование в общем похоже на этот пример, с той лишь разницей, что операция XOR заменяется линейной комбинацией данных, интерпретируемых как числа из конечного поля (необходимые сведения из алгебры будут приведены ниже). Сетевое кодирование повышает эффективную пропускную способность сети, оно также подходит для тех случаев, когда решение принимается на основе неполной или неопределенной информации. Подобно кодированию в каналах со стиранием успешный прием информации здесь не зависит от получения специфического содержания пакета, а скорее от получения достаточного количества независимых пакетов. Следует, конечно, отметить, что сетевое кодирование требует повышенных вычислительных возможностей узлов. Однако закон Мура приводит к понижению стоимости вычислений, а проблемы современных сетей вызываются в основном недостаточной пропускной способностью. Таким образом, линейное кодирование использует дешевые вычислительные мощности для увеличения эффективности сетей. Для понимания дальнейшего нам необходимы некоторые сведения из абстрактной алгебры, приведенные здесь в минимальном объеме и без излишней строгости. Конечные поляМожно было бы сразу дать определение конечного поля, однако для удобства дальнейшего изложения введем сначала понятие группы. Прежде всего приведем следующее: Определение 1. Соответствие, в силу которого каждой паре а и b элементов множества М, взятых в данном порядке, соответствует третий элемент с того же множества М, называется алгебраической операцией, определенной в М. Обычно это записывается в виде ab = c. Примерами алгебраических операций могут служить четыре известных арифметических действия на множестве всех действительных чисел, причем в случае деления нужно исключить число 0. В одном и том же множестве может быть задано несколько алгебраических операций. Рассматривая множества с одной алгебраической операцией, мы приходим к первому из основных понятий современной алгебры – к понятию группы. Определение 2. Непустое множество G называется группой, если в нем определена алгебраическая операция, называемая умножением, которая каждым двум элементам a и b из G ставит в соответствие элемент ab = с также из G, называемый их произведением. Выполняются также следующие аксиомы:
Если для любых двух элементов группы a и b выполняется равенство ab = ba, то такая группа называется коммутативной, или абелевой. Часто групповая операция в коммутативных группах обозначается знаком «+», и группу называют аддитивной. Примерами могут служить все целые, все рациональные и все действительные числа с операцией арифметического сложения, играющего роль групповой операции умножения. Другой простой пример группы – множество всех рациональных (и действительных) чисел (исключая число 0) с операцией арифметического умножения. Опираясь на понятие группы, приведем теперь упрощенное определение поля. Определение 3. Непустое множество F называется полем, если в нем определены две алгебраические операции: сложение и умножение, такие, что для них выполняются все свойства соответствующих арифметических операций (коммутативность и ассоциативность относительно сложения, коммутативность и ассоциативность относительно умножения, дистрибутивность умножения относительно сложения), и все элементы F являются группой относительно сложения, а все ненулевые элементы F – группой относительно умножения. Называются они соответственно аддитивной и мультипликативной группами поля F. Полями, как нетрудно видеть, являются множества всех рациональных и действительных чисел со сложением и умножением в качестве алгебраических операций. Нам понадобится еще определить отношение эквивалентности на множестве целых чисел, которое называется сравнением по модулю натурального числа. Определение 4. Говорят, что два целых числа a и b сравнимы по модулю натурального числа n и записывают a = b (mod n), если при делении на n они дают одинаковые остатки. К примеру, 7 = 2 (mod 5). Теперь мы располагаем всем необходимым, чтобы рассмотреть некоторые свойства полей с конечным количеством элементов, или конечных полей. Их также называют полями Галуа (в честь французского математика Эвариста Галуа, который ввел их впервые) и обычно обозначают GF(q), где q – число элементов поля. Можно показать, что число элементов конечного поля всегда имеет вид q = = pn, где р – простое число, называемое характеристикой, а n – натуральное. Обратимся к некоторым полезным для дальнейшего примерам конечных полей. Поле GF(2) содержит два элемента: 0 и 1. Операции в этом поле определяются следующим образом: 0 + 0 = 1 + 1 = 0, Как видно, алгебраическая операция сложение и обратная ей вычитание идентичны и выполняются посредством оператора XOR, а умножения – AND. Поскольку 1 является единственным обратным элементом в мультипликативной группе, то операция деления совпадает с умножением. Рассмотрим теперь операции в поле GF(7). Его элементами являются числа 0, 1, 2, ... , 6. Алгебраические операции сложения и умножения выполняются по правилам модульной арифметики. То есть 3 + 5 = 1 (mod 7), Может показаться, что обратным элементом, скажем для 3 в аддитивной группе, будет число -3, поскольку 3 + (- 3) = 0. Однако число -3 не является элементом поля. Алгоритм нахождения обратного для элемента q в аддитивной группе достаточно прост. Нужно складывать q с каждым элементом поля до тех пор, пока не получим число, делящееся на характеристику без остатка. В нашем случае это будет 4, поскольку 3 + 4 = = 0 (mod 7). Аналогичный алгоритм для нахождения обратного элемента в мультипликативной группе: 3 × 5 = 1 (mod 7). То есть 5 является обратным к 3 и наоборот. Для дальнейшего особо интересны поля типа GF(2n). Их элементы могут быть представлены в виде двоичных чисел. Для поля GF(28) это будут октеты, или байты, к примеру {01010011}, {11001010} и т. п. Операция сложения выполняется посредством применения оператора XOR к битам, находящимся на одинаковых позициях: {01010011} + + {11001010} = {10011001}. Элементы GF(2n) могут быть также представлены полиномами степени строго меньшей, чем n, с коэффициентами из GF(2n). Операции над полиномами выполняются по модулю R , где R – неприводимый (т. е. не разлагающийся на множители) полином над GF(2n) степени n. Сложение выполняется обычным методом с приведением коэффициентов по модулю 2. Умножение двух полиномов P и Q может быть выполнено следующим образом. Сначала находится их произведение W = P • Q, а затем вычисляется остаток по модулю R. Для поля GF(28) первому двоичному символу из вышеприведенного примера соответствует полином x6 + x4 + x + 1, а второму – полином x7 + x6 + x3 + x. Примером неприводимого полинома для этого поля может служить x8 + x4 + x3 + x + 1. На этом мы окончим необходимое математическое вступление и перейдем непосредственно к вопросу... ...Что такое сетевое кодирование?Для наших целей достаточно ограничиться линейным сетевым кодированием. Рассмотрим систему, действующую как ретранслятор информации, такой как маршрутизатор, узел в произвольной сети или узел в одноранговой распределенной сети. Обычно, когда пакет с данными достигает некоторого другого узла, тот просто повторяет его. Как уже упоминалось выше, при сетевом кодировании предполагается, что узел образует некую комбинацию из полученных пакетов и создает один или несколько выходных пакетов. Предположим, что каждый пакет содержит L бит. Если комбинируемые пакеты имеют не одинаковые размеры, то меньшие дополним хвостовыми нулями. Мы будем интерпретировать s последовательных битов пакета как символ над полем GF(2s), а каждый пакет – как вектор, содержащий L/s символов. При линейном кодировании выходной пакет является линейной комбинацией полученных пакетов, где операция сложения выполняется над полем GF(2s). Смысл выбора линейной комбинации заключается в том, что при этом алгоритмы кодирования и декодирования весьма прозрачны. Следует заметить, что линейная комбинация пакетов не является их конкатенацией: если мы образуем линейную комбинацию пакетов длины L, то результирующий пакет также имеет длину L. Рассмотрим теперь непосредственно процедуру линейного кодирования. Предположим, что исходные пакеты М1, ..., Мn генерируются одним или несколькими источниками. При линейном сетевом кодировании каждый пакет, проходящий через сеть, связан с последовательностью коэффициентов g1, ...gn, i из поля GF(2s) (т. е. gi является символом из s бит) и равен:
где суммирование выполняется по каждой позиции символа. Другими словами,
где Xk и Положим для упрощения, что передаваемый пакет содержит как коэффициенты g = (g1, ... , gn), называемые кодирующим вектором, так и закодированные данные:
называемые информационным вектором. Кодирующий вектор используется приемником для декодирования данных (о чем несколько ниже). Например, если кодирующий вектор ei = (0, ... , 1, 0, ... , 0), т. е. содержит 1 в m-й позиции (единица поля GF(2s)), то информационный вектор равен Mm, а значит – не закодирован. Кодирование может выполняться рекурсивно, а именно, применяться к уже закодированным пакетам. Рассмотрим теперь вкратце принципы декодирования. Предположим, узел получил набор закодированных пакетов (g1, X1), ... , (gm, Xm). Для того чтобы извлечь оригинальные пакеты, необходимо решить систему m уравнений:
j = {1, ... , m}, в которой неизвестными являются Mi. То есть требуется решить систему m уравнений с n неизвестными. Для восстановления всех данных необходимо, чтобы m≥ n, т. е. число полученных пакетов, должно быть не меньше, чем число оригинальных пакетов. Однако это условие недостаточно, поскольку среди комбинаций могут быть линейно зависимые. Поэтому одной из проблем разработки сетевого кодирования является выбор линейных комбинаций, выполняемый каждым узлом. Самый простой алгоритм заключается в том, чтобы каждый узел независимо и децентрализованно выбирал произвольно с равной вероятностью элементы поля GF(2s). Однако в этом случае существует определенная вероятность выбора линейно зависимых комбинаций. Эта вероятность зависит от числа элементов поля. Оценки показывают, что даже для полей с небольшим количеством элементов (например, s = 8) она пренебрежимо мала. Альтернативный подход заключается в детерминистических алгоритмах выбора комбинаций. Так, разработаны алгоритмы для многоадресных рассылок с полиномиальным временем работы, которые последовательно рассматривают узлы сети и решают, какую линейную комбинацию должен выбрать каждый из них. Так как любой из узлов использует фиксированный набор коэффициентов, то передавать необходимо только информационный вектор. Как уже упоминалось выше, декодирование требует решения системы линейных уравнений. На практике это может быть выполнено следующим образом. Узел хранит закодированные векторы, которые он получает, а также собственные оригинальные пакеты строка за строкой в так называемой декодирующей матрице. Первоначально в ней содержатся только незакодированные (оригинальные) пакеты, которые этот узел должен отослать, и соответствующий кодирующий вектор. Когда поступает закодированный пакет, он вставляется в качестве последней строки в декодирующую матрицу. Затем матрица преобразуется к треугольному виду с помощью метода исключения Гаусса. Как только в матрице получится строка в форме ei, то этот узел знает, что x равен оригинальному пакету Mi. Это происходит в самом конце, когда получено n линейно независимых закодированных векторов. Заметим, что декодирование выполняется не всеми узлами сети, а только получателями. Какова польза от сетевого кодирования?Основная причина, по которой вспыхнул интерес к сетевому кодированию, заключалась в том, что оно может увеличить емкость сети при многоадресной рассылке.
Представим сеть как ориентированный граф (в типичном случае это проводная сеть). Пусть вершины графа соответствуют терминалам, а ребра – каналам. Предположим, что у нас имеется М источников, каждый из которых посылает данные при некоторой заданной скорости, и N приемников. Все приемники хотят принимать пакеты от всех источников. Приведем весьма интересную теорему и примем ее без доказательства. Теорема. Предположим, что скорости передачи пакетов источниками таковы, что без сетевого кодирования сеть может изолированно поддерживать любой из приемников (т. е. этот приемник может получать пакеты всех источников, как если бы он был единственным в сети). Тогда при подходящем выборе коэффициентов линейного кодирования сеть может поддерживать все приемники одновременно. Другими словами, когда N приемников разделяют сетевые ресурсы, каждый из них может получать пакеты на максимальной скорости, как будто бы он находится в сети один. Таким образом, сетевое кодирование помогает эффективней использовать сетевые ресурсы. Это проиллюстрировано на рис. 2, на котором представлена сеть, называемая «бабочкой». Все каналы имеют емкость 1, т. е. могут за один цикл передать только один бит. Источник S передает два бита b1 и b2 приемникам Y и Z. Так как канал от W к X может за один цикл передать лишь один бит, то в сети без кодирования (рис. 2, а) для пересылки b2 узлу Y необходим еще один цикл. В сети с кодированием (рис. 2, б) узел W выполняет над полученными битами операцию XOR и передает результирующий пакет узлу X , который пересылает его приемникам. Узел Y, имея b1, декодирует пакет и извлекает b2. Точно так же поступает и узел Z. Таким образом выигрывается один цикл. Сетевое кодирование может обеспечивать повышение пропускной способности сети не только в случае многоадресных потоков, но также и для одноадресных. Особенно эффективно сетевое кодирование для обеспечения надежности и адаптивности сети. Обратимся снова к рис. 1 и предположим, что узлы A и B могут переходить в спящий режим или выйти за зону досягаемости без оповещения станции S. Если базовая станция S широковещательно передает пакет a (или b), он может быть полностью потерян, так как адресат может его не получить. Однако если базовая станция широковещательно отправит пакет a XOR b или, более общо, случайную линейную комбинацию информационных пакетов, передача доставит новую информацию всем активным узлам. Вероятно, одним из наиболее известных приложений, использующих сетевое кодирование, является одноранговая (peer-to-peer) сеть Avalanche. В ней файл, который должен распределяться, расщепляется на небольшие блоки. Однако узлы вместо простой передачи блоков передают их случайную линейную комбинацию вместе со случайными коэффициентами данной линейной комбинации. Этим устраняется необходимость для каждого узла иметь полную информацию о распределении блоков в сети. Небольшое заключениеКонечно, читатель вправе высказать некоторое недоумение по поводу того, что статья несколько перегружена математикой. С другой стороны, для понимания, что представляют собой современные сети, полезно знать, как уже упоминалось выше, что это не только оптоволоконные и медные кабели, радиопередатчики, коммутационные фабрики, порты и интерфейсы, но и весьма изысканная математика. Представьте себе, аппарат, созданный для исследования проблемы решения алгебраических уравнений в радикалах в 1831 г., более чем через 170 лет находит применение в информационных технологиях. В связи с этим необходимо сказать несколько слов о его создателе, безусловно гениальном французском математике Эваристе Галуа (род. в 1811 г.), жизнь которого можно сравнить с падающей звездой. В возрасте 20 лет он дал исчерпывающий ответ на вопрос, три века бывший вызовом для математиков всего мира. Хотя понятие группы впервые появилось в работах Лагранжа и Руфини, сам термин «группа» был введен Галуа. Его идеи оказались плодотворными во всех областях математики и теоретической физики. Он погиб на дуэли в 1832 г., причем ни причина дуэли, ни его противник достоверно неизвестны. Стратегія охолодження ЦОД для епохи AI
Читайте также
|
Останні обговоренняТОП-новости
ТОП-блогиТОП-статьи
|
||||||||||||||||





Несколько замечаний по статье.
1.Передача данных по защищенным каналам связи или с использованием средств криптографии вряд ли возможна ("в лоб") данными алгоритмами.
2.Не все устройства делают широковещательную рассылку. Статья (скорее всего) ориентирована на беспроводные коммуникации (но явно об этом не указывается).
3.Делать сравнения эффективности на основе одного бита при существенно больших размерах пакетов (+ достаточно больших накладных расходах на служебные данные) по меньшей мере странно.
4.Схемы, в которых получатель еще и ретранслятор (т.е. маршрут неизвестен) обычно изначально обладают очень многими недостатками. И решаемая для них задача ускорения посылки пакета не первоприоритетная.
P.S.
Вы вспомнили Галуа, но забыли про Клода Шеннона, рассказали о возможном выигрыше, но не упомянули проект Iamanet (intrinsically assurable mobile ad-hoc networking) BAE Systems ...
В принципе, это переведення статья Кристины Фрагули, Жана-Ива Ле Буде и Йорга Видмера, Network Coding: An Instant Primer, с добавкой замечаний про Галуа и его конечные поля. Те части, где объясняется сетевое кодирование, переведены дословно. Так что особой научной работы автора здесь нет, а выше приведенные вопросы - не к нему. ;)