Компьютер сгенерировал математическое доказательство объемом 200 ТБ

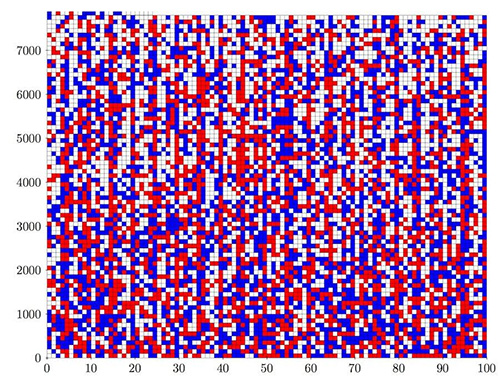
Трое исследователей, Марийн Хойле (Marijn Heule) из Техасского университета, Оливер Куллманн (Oliver Kullmann) из Государственного университета Уэльса (Великобритания) и Виктор Марек (Victor Marek) из университета Кентукки получили доказательство ошибочности гипотезы булевых троек Пифагора. Для этого им потребовалось двое суток машинного времени суперкомпьютера Stampede Техасского центра продвинутых вычислений. В текстовом виде доказательство занимает 200 ТБ — своеобразный рекорд в математической практике.

Эта математическая гипотеза является частью теоремы Рамсея и была сформулирована в 1980-е годы Рональдом Грэхемом (Ronald Graham), который установил символический приз в $100 за её решение. Она предполагает, что возможно раскрасить каждое неотрицательное целое число в один из двух цветов (синий или красный), так, чтобы ни одна из троек, удовлетворяющих формуле Пифагора (a² + b² = c²), не была бы полностью одноцветной.

Авторам удалось существенно оптимизировать вычислительную задачу и свести количество анализируемых на 800 процессорных ядрах Stampede вариантов раскраски к одному триллиону с первоначальных 10²³⁰⁰. В итоге было показано, что целые числа можно раскрасить требуемым образом, но только до 7824. Начиная с 7825 гипотеза Грэхема становится ошибочной.

Технически, команда математиков заслужила свой приз, но многие задаются вопросом, можно ли механический перебор вариантов считать доказательством. По-прежнему непонятно, почему допущение перестаёт работать именно на этом числе, и почему вообще существует область, где оно справедливо.

Кроме того, если никто и никогда, кроме, опять же, компьютерных программ, не сможет прочесть генерируемые машинами доказательства, напрашивается вопрос, а существуют ли они в философском смысле?

Стратегія охолодження ЦОД для епохи AI