Maxima: максимум удобства и функциональности
27 апрель, 2004 - 23:00Константин НосовСистема компьютерной математики Maxima -- настоящий ветеран среди программ этого класса. Она старше многих своих известных коммерческих собратьев по крайней мере на два десятка лет. Первоначально носившая имя Macsyma, она была создана в конце 1960-х годов в знаменитом Массачусетском технологическом институте и почти 20 лет (с 1982 по 2001) поддерживалась Биллом Шелтером (William Schelter), благодаря которому и приобрела свои замечательные качества и известность в научном мире. Подробности по истории системы, инсталляционный модуль (размером всего в 10 MB), документацию, исходный код и другую сопутствующую информацию можно найти на Web-узле пакета http://maxima.sourceforge.net. Текущая версия (5.9.0) работает под управлением Windows и Linux.
Несмотря на скромные размеры, Maxima -- высокоинтеллектуальный продукт, способный решать сложные аналитические задачи. Как и большинство систем компьютерной математики, она является командным интерпретатором, взаимодействующим с пользователем по принципу "вопрос -- ответ". Поэтому рабочая область системы представляет собой последовательность ячеек ввода/вывода (рис. 1), маркированных меткой (С -- для ввода пользователя, D -- для результата) и номером. Такой способ обозначения обеспечивает удобный механизм ссылок, позволяющий для обращения к одному из предыдущих результатов ввести только имя нужной ячейки.
Численные операции

|
| Рис. 1 |
Для расчетов с высокой точностью Maxima поддерживает специальные операторы, позволяющие вычислить любое значение с произвольной разрядной сеткой (в пределах, естественно, аппаратных возможностей). Это относится и к целым числам: их величина в системе программно не ограничена. К тому же Maxima имеет очень приличную скорость работы с арифметикой высокой точности, что дает возможность проводить вычисления с целыми числами в десятки и сотни тысяч разрядов с производительностью на уровне лучших коммерческих систем.
Отметим, что Maxima взвешенно подходит к регистру вводимых выражений. Если их вид близок к имени встроенной функции, программа использует эту функцию. Согласно данному правилу Sin, sin и SIN обозначают одно и то же. Вместе с тем пользовательские переменные и функции чувствительны к регистру -- X и x могут обозначать разные объекты.
Система также поддерживает комплексную арифметику и ряд известных математических констант.
Аналитические операции
|
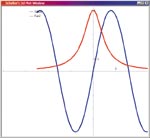
| Рис. 2 |
В случае если для введенного выражения нельзя получить однозначный результат, программа практически на естественном (английском) языке задаст наводящие вопросы. К примеру, при попытке найти интеграл от функции xn Maxima уточнит, не равно ли n+1 нулю (как известно, от этого существенно зависит результат). Впрочем, таких вопросов можно избежать, если заранее с помощью специальных операторов указать область изменения используемых параметров и переменных.
Аналитический аппарат также поддерживает алгебраические операции с полиномами (деление двух полиномов, вычисление наибольшего общего делителя, разложение на множители) и тригонометрическими выражениями. Для практических приложений большую роль играют заложенные в систему инструменты решения уравнений и систем различных типов -- алгебраических, трансцендентных и дифференциальных.
Операции линейной алгебры
В Maxima реализован весьма совершенный механизм векторно-матричных операций, позволяющий проводить сложные алгебраические вычисления. Матрицы вводятся универсальным оператором matrix, затем к ним применимы обычные линейные операции -- сложение, вычитание, умножение на скаляр (для их записи используют естественную математическую нотацию вроде A+B), а также транспонирование, обращение, вычисление определителей, спектральных характеристик и пр.
Графические возможности

|
| Рис. 3 |
Средства программирования
Как и всякая система компьютерной математики, Maxima позволяет создавать сложные программы и использовать их в задачах, решение которых с помощью командной строки может оказаться сложным и неэффективным.
В самом простом случае пользовательская функция определяется прямо в командной строке
MyFunc(x,y):=x^2+y^2; |
Затем MyFunc можно применять наряду со встроенными. Конечно же, система поддерживает и более сложные конструкции. В теле функции допускаются операторы ветвления, циклов, ввода/вывода и т. д. Язык программирования в Maxima имеет некоторые особенности, важнейшей из которых является то, что число аргументов функции не обязано быть фиксированным. Другая состоит в чрезвычайно гибких средствах для работы с массивами, которые редко встретишь не только в традиционных языках, но и специализированных системах, в том числе СКМ. Вот несколько примеров, заимствованных из одного руководства (двоеточие в Maxima означает присваивание):
a[4]:4*u; |
Все операторы корректны и задают в совокупности массив, индексами которого служат числа 4, 22/7 и строка "x", а значениями элементов -- выражение 4*u, число π (в Maxima оно записывается как %PI) и строка символов "mystery". Таким образом, как элементом массива, так и его индексом может выступать практически любое выражение. Оригинальные свойства Maxima вовсе не ограничиваются этими особенностями (например, поддерживаются даже массивы функций), но мы не будем останавливаться на деталях.
Вообще, Maxima написана на языке Lisp и непосредственно поддерживает многие его команды. Можно сказать, что Lisp является ядром системы, и к нему допускается обращаться при "низкоуровневом" программировании. Впрочем, в большинстве случаев этого не требуется. Maxima предоставляет достаточное количество уже готовых средств, использовать которые значительно проще, чем Lisp-операторы.
При необходимости программы сохраняются во внешних файлах. Команды записываются в том же виде, в каком они вводятся в систему, имеются лишь некоторые особенности для оформления функций.
Забота о пользователе
Кроме документации, доступной на Web-узле продукта, в комплект поставки входят введение в Maxima и учебник по системе (оба в формате HTML) -- детальное описание, достаточное для углубленного ознакомления со всеми ее возможностями. Однако во время сеанса работы с системой нередко необходимо получить оперативную справку. Для этого Maxima предоставляет функцию DESCRIBE(), которая выводит подробные сведения об интересующем пользователя операторе (который передается ей в качестве аргумента). Не беда, если вы не помните его полный синтаксис, введите несколько первых букв названия -- и Maxima выдаст все доступные имена, начинающиеся с данной комбинации символов. Если же этих сведений окажется недостаточно, то можно воспользоваться функцией EXAMPLE(), которая предложит характерные примеры. К функциям этого же ряда принадлежит DEMO(), выполняющая программы из демонстрационных файлов, поставляемых с системой. Хотелось бы отметить такую особенность системы, как возможность представления результатов вычислений в формате TeX с помощью функции, которая так и называется -- TEX().
Выводы
Надеемся, что после этого небольшого материала у читателей все же сложилось представление о Maxima как о действительно профессиональной системе, предназначенной для решения сложных численных и аналитических задач, а также графического представления данных. Особенно, как было отмечено вначале, программа сильна в аналитических расчетах и арифметике высокой точности. Конечно, Maxima далеко не совершенна, и по многим аспектам не дотягивает до коммерческих продуктов вроде Maple и Mathematica. Однако это не умаляет ее достоинств -- Maxima вполне можно использовать и в учебных целях, и в качестве платформы для вполне серьезных научных разработок.